

Continue as long as all the elements in that particular boundary get rotated in 90 0 anticlockwise directions. Then take the next 4 elements along the edges(left, right, top, bottom) and swap them in an anticlockwise direction. For each boundary take the 4 corner elements and swap them such that the 4 corner elements get rotated in anticlockwise directions. , rotation by, as a matrix using Theorem 17: R cos() sin() sin() cos() 1 0 0 1 Counterclockwise rotation by 2 is the matrix R 2 cos( 2) sin() sin( 2) cos( 2) 0 1 1 0 Because rotations are actually matrices, and because function composition for matrices is matrix multiplication, we’ll often multiply.Iterate over all the boundaries in the matrix.There are such (n/2-1) boundaries in the matrix. The idea is to traverse along the boundaries of the matrix and shift the positions of the elements in 90 0 anticlockwise directions in each boundary. And this is the Givens transformation with the condition that a 12, a 13, a 14, a 23, a 24, a 34.are all >0. To learn about Matrix Rotation please click on any of the Theory Guide links in Section 2 below. The space complexity is constant as no extra space is required.Īnother Approach using a single traversal of the matrix : Multiplying the Matrix A by a rotation Matrix with this angle eliminates a 12 and if we perform the same calculation with. The matrix is traversed twice, so the complexity is O(R*C). ISRO CS Syllabus for Scientist/Engineer Exam.We have the formula for the three angles of rotation below: R o t a t i o n 90 : R 90 ( x, y) ( y, x) R o t a t i o n 180 : R 180 ( x, y. The most common rotation angles are 90 degrees, 180 degrees, 270 degrees etc. Rotation can be done clockwise as well as counterclockwise. ISRO CS Original Papers and Official Keys The rotation turns the circle through an angle.GATE CS Original Papers and Official Keys.
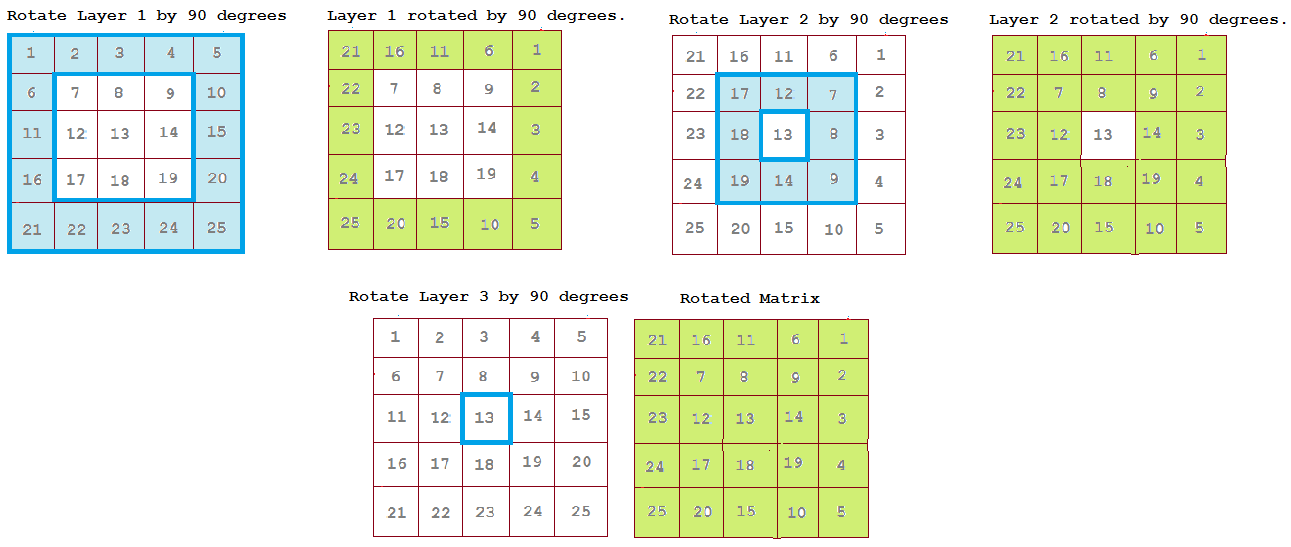
Rather than look at the vector, let us look at its x and y components and rotate them (counterclockwise) by. The elements in the current group is (x, y), (y, N-1-x), (N-1-x, N-1-y), (N-1-y, x), now rotate the these 4 elements, i. The rotation matrix can be derived geometrically. Will this also work for NN matrix rotation by 90 degrees The time complexity is O(N) since it just traverse the input matrix and copy it to the new matrix. That is, for each vector vin R2, R(v) is the result of rotating vby radians (in the counter-clockwise direction). So run a loop in each cycle from x to N - x - 1, loop counter is yĤ. Rotations of the Plane R2 Let R2R R2 be the transformation of R2 given by rotating by radians (in the counter-clockwise direction about 0). So the number of such groups in a cycle is N - 2 * i.ģ. Consider elements in group of 4 in current square, rotate the 4 elements at a time. Run a loop to traverse the matrix a cycle at a time, i.e loop from 0 to N/2 - 1, loop counter is iĢ. There is N/2 squares or cycles in a matrix of side N. The idea is for each square cycle, swap the elements involved with theĬorresponding cell in the matrix in clockwise direction one at a time using nothing butġ. Is formed by 2nd row, second-last column, second-last row and 2nd column. The first cycle is formed by its 1st row, last column, last row and 1st column. We have presented two approaches to find the two elements: Īpproach 1: To solve the question without any extra space, rotate the array in form of squares, dividing the matrix into squares or cycles.įor example, A 4 X 4 matrix will have 2 cycles. (I say matrix-based because quaternions are faster and more flexible than matrix rotations. Matrix rotation: Given a matrix, rotate the matrix 90 degrees clockwise. Axis-angle rotations are the most useful matrix-based rotation.


 0 kommentar(er)
0 kommentar(er)
